How to Find Moment of a Bearing on a Shaft

You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.

• Forums
• Engineering
• General Engineering

Moment and reaction of shaft - Statically Indeterminate

• Thread starter Tekneek
• Start date Oct 18, 2015

A shaft of diameter 10 inch is supported by 3 ball bearings. An external force (F, given) from pulley (diameter not given) also acts on the shaft. The supports are subjected to bending load (moment and transverse shear) and torsion load due to pulley. Yield Stress at Tension given. Assume no axial load. I need to calculate the reactions and moment equation for the shaft.

My approach:

• Statically Indeterminate

(1) ∑Fy = 0 = Ra + Rb + Rc -F
(2) ∑Mc (CCW +) = 0 = 5F-6Ra-3Rb
Solve (2) for Rb and Plug it in (1)

To write a moment equation, I make a cut between Rb and Rc
Summing the moment at the Cut (o)
∑Mo = 0 = -Ra(x) -Rb (x-2) + F(x-1) + M = 0
(3) M = Ra(x) + Rb(x-2) - F(x-1)

After this I can calculate the reactions using deflection method (singularity equation).

However, I am not sure that my moment equation is correct. Since the problem states that the shaft is subjected to bending load and torsion load at the ball bearings, do I have to account for these in my moment equation? If so, how?

Answers and Replies

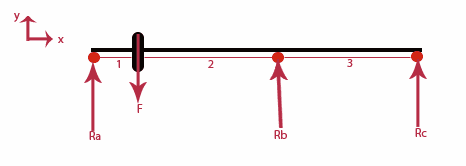
A shaft of diameter 10 inch is supported by 3 ball bearings. An external force (F, given) from pulley (diameter not given) also acts on the shaft. The supports are subjected to bending load (moment and transverse shear) and torsion load due to pulley. Yield Stress at Tension given. Assume no axial load. I need to calculate the reactions and moment equation for the shaft.

My approach:

• Statically Indeterminate

(1) ∑Fy = 0 = Ra + Rb + Rc -F
(2) ∑Mc (CCW +) = 0 = 5F-6Ra-3Rb
Solve (2) for Rb and Plug it in (1)

To write a moment equation, I make a cut between Rb and Rc
Summing the moment at the Cut (o)
∑Mo = 0 = -Ra(x) -Rb (x-2) + F(x-1) + M = 0
(3) M = Ra(x) + Rb(x-2) - F(x-1)

After this I can calculate the reactions using deflection method (singularity equation).

However, I am not sure that my moment equation is correct. Since the problem states that the shaft is subjected to bending load and torsion load at the ball bearings, do I have to account for these in my moment equation? If so, how?

Assuming the shaft is free to rotate in the ball bearings, the torsion load should not affect the bearing reactions.

It's not clear to me how you have derived your moment equations. Are there some lengths of shaft segments which are not included in this thread?

In any event, the bearing reactions are produced only by the transverse loading of the shaft. There is a concentrated load due to the tension on the pulley (F), and I think you want to include the weight of the shaft as a distributed load, since the shaft is 10 inches in diameter. Once these transverse loads are figured, there are several different techniques which can be used to calculate the bearing reactions, including singularity functions.

Assuming the shaft is free to rotate in the ball bearings, the torsion load should not affect the bearing reactions.

It's not clear to me how you have derived your moment equations. Are there some lengths of shaft segments which are not included in this thread?

In any event, the bearing reactions are produced only by the transverse loading of the shaft. There is a concentrated load due to the tension on the pulley (F), and I think you want to include the weight of the shaft as a distributed load, since the shaft is 10 inches in diameter. Once these transverse loads are figured, there are several different techniques which can be used to calculate the bearing reactions, including singularity functions.

Sorry, that was my fault.
∑Mo = 0 = -Ra(x) -Rb (x-3) + F(x-1) + M = 0
(3) M = Ra(x) + Rb(x-3) - F(x-1)

Using singularity function

dy/dx = 1/EI [ (Ra(x-0)^2 )/2 + (Rb(x-3)^2)/2 - (F(x-1)^2)/2 + C1 ]
y(x) = 1/EI [ (Ra(x-0)^3 )/6 + (Rb(x-3)^3)/6 - (F(x-1)^3)/6 + C1x + C2 ]

Applying Boundary Condition
@x=0, dy/dx = 0 --> C1 = 0

@x=3, y(0) = 0 --> 0 = 4.5Ra - 267 + C2
@x=3, dy/dx = 0 --> 0 = 13.5Ra - 400 --> Ra = 29.62

Then using Ra I can find C2, then using that information I can find Rb and finally Rc. Am I correct so far?

Sorry, that was my fault.
∑Mo = 0 = -Ra(x) -Rb (x-3) + F(x-1) + M = 0
(3) M = Ra(x) + Rb(x-3) - F(x-1)

Using singularity function

dy/dx = 1/EI [ (Ra(x-0)^2 )/2 + (Rb(x-3)^2)/2 - (F(x-1)^2)/2 + C1 ]
y(x) = 1/EI [ (Ra(x-0)^3 )/6 + (Rb(x-3)^3)/6 - (F(x-1)^3)/6 + C1x + C2 ]

Applying Boundary Condition
@x=0, dy/dx = 0 --> C1 = 0

@x=3, y(0) = 0 --> 0 = 4.5Ra - 267 + C2
@x=3, dy/dx = 0 --> 0 = 13.5Ra - 400 --> Ra = 29.62

Then using Ra I can find C2, then using that information I can find Rb and finally Rc. Am I correct so far?

No, that's not how this works.

Your shaft is a continuous beam, since it rests on more than two supports. As a continuous beam, the equations of static equilibrium are insufficient to determine the reactions in the supports. Without figuring out the reactions first, you don't have enough equations to determine the integration constants for the slope and deflection of the shaft.

Have you studied anything about continuous beams and how to calculate the reactions at the supports?

No, that's not how this works.

Your shaft is a continuous beam, since it rests on more than two supports. As a continuous beam, the equations of static equilibrium are insufficient to determine the reactions in the supports. Without figuring out the reactions first, you don't have enough equations to determine the integration constants for the slope and deflection of the shaft.

Have you studied anything about continuous beams and how to calculate the reactions at the supports?

Not exactly sure. If you could link me to something I could look up that would be helpful.

Not exactly sure. If you could link me to something I could look up that would be helpful.

Google "continuous beam" and you'll get enough hits to keep you busy into next week.

Related Threads on Moment and reaction of shaft - Statically Indeterminate

• Last Post
• Jan 25, 2005

• Last Post
• Jul 25, 2011

• Last Post
• Nov 30, 2007

• Last Post
• Jul 7, 2005

• Last Post
• Jul 28, 2015

• Last Post
• Mar 14, 2009

• Last Post
• Feb 21, 2012

• Last Post
• Aug 5, 2009

• Last Post
• Oct 19, 2012

• Last Post
• Mar 11, 2012

• Forums
• Engineering
• General Engineering

How to Find Moment of a Bearing on a Shaft

Source: https://www.physicsforums.com/threads/moment-and-reaction-of-shaft-statically-indeterminate.838401/

Share this post